回帰分析　～風速5m で桶屋はいくら儲かる？～

今回はデータ分析編第2弾、『回帰分析』についてお話していきます。
　※前回記事はこちら⇩

---

回帰分析

回帰分析とは、「影響を与える値」から「影響を与えられる値」への関係性を分析する手法のことをいいます。

回帰分析では、「影響を与えられる値」を『目的変数』と呼び、目的変数に「影響を与える値」を『説明変数』と呼びます。また、説明変数を変数X、目的変数は変数Yで表されることが多いです。

つまりは以下の通りです。
　影響を与えられる値    ＝　目的変数＝Y
　影響を与える値   　　 ＝　説明変数＝X

さて『「影響を与える値」から「影響を与えられる値」への関係性』とは、「変数Xが変数Yに影響を与える」という因果関係のことです。

つまり、回帰分析は「変数X→変数Y」の因果関係を分析者が仮定した上で分析を行います。

質的変数と量的変数

具体的な話に入る前に、回帰分析の手法が変わってくるため、変数について少し説明します。

○変数とは
変数とは、データ分析に用いるデータの各項目を指しています。
変数には、以下の2つの種類があります。

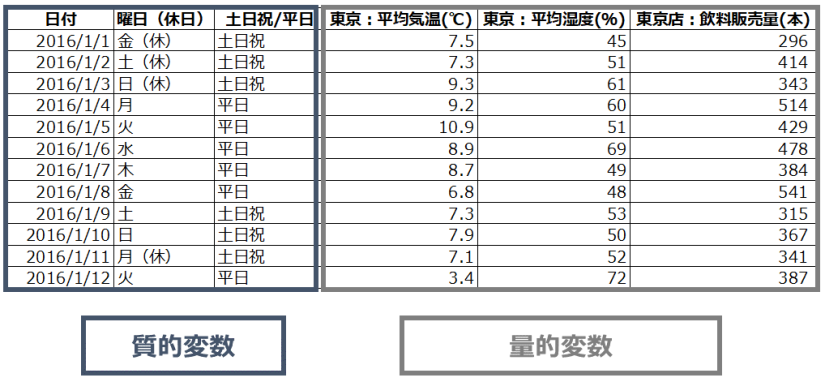
○質的変数
質的変数は、種類を区別する変数のことです。
例えば、アンケートの満足度(大変満足、満足、普通、不満、大変不満)や、名前や住んでいる都道府県などのことです。
これらは数値ではないため、分析に取り入れるときには、ダミー変数というものを導入します。（※後述）

○量的変数
量的変数は、データが数値で示されるもののことです。
例えば、身長、体重、気温などのことです。

---

---

回帰分析の実践

前置きが長くなりましたが、ここからが回帰分析の実践編です。

回帰分析は、「説明変数」が1つの場合を「単回帰分析」、複数の場合を「重回帰分析」といいます。
それぞれ、分析を行うことで以下のように数式化されます。

---

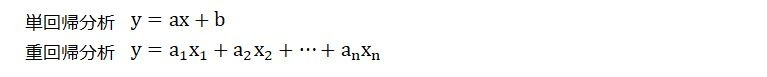
この数式のことを「回帰式」といいます。
また、xや「x1,x2,…,xn」の前についている、aや「a1,a2,…,an」のことを回帰係数といいます。

○回帰分析でできること
回帰分析は、主に以下の2つのことができます。

１．予測
回帰分析では上記のように、数式化できるため、変数Y(未来)を予測することができます。

２．効果検証
これまでのデータでの、原因（説明変数）から結果（目的変数）への効果の検証ができます。

～～～～～～～～
○エクセルでの回帰分析
エクセルで簡単に回帰分析をする場合は、「分析ツール」をアドインする必要があります。
エクセル上部の「データ」タブに『データ分析』という項目がない方は、以下を参考にアドインしてください。

「Excel で分析ツールPak を読み込む」
～～～～～～～～

○単回帰分析の例
次のデータは、「東京の1日の平均気温と飲料販売数」を表した散布図です。
（「総務省 ICTスキル総合習得プログラム　コース3（データ分析）」のデータを参照）

---

---

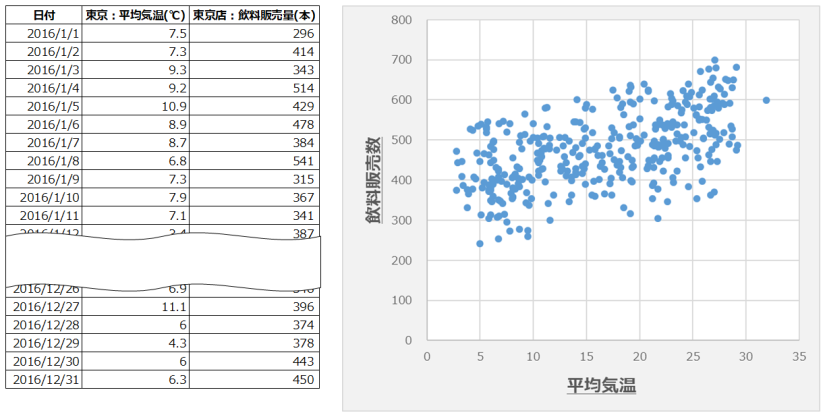
飲料販売数を目的変数Y、平均気温を説明変数Xとするとき、回帰式を求めると以下のようになります。

（飲料販売数） = 6.4205＊（平均気温） + 370.87

この回帰式は、アドインの「データ分析」でも算出できますが、上記の散布図からも「グラフの要素」として追加ができます。

---

---

---

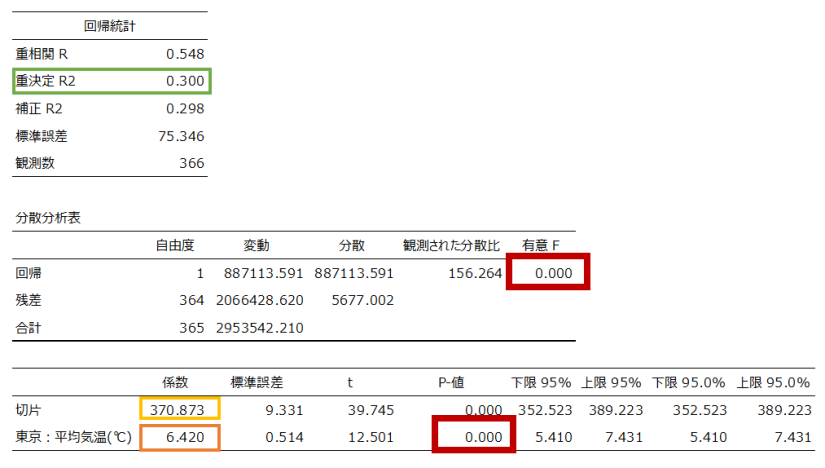
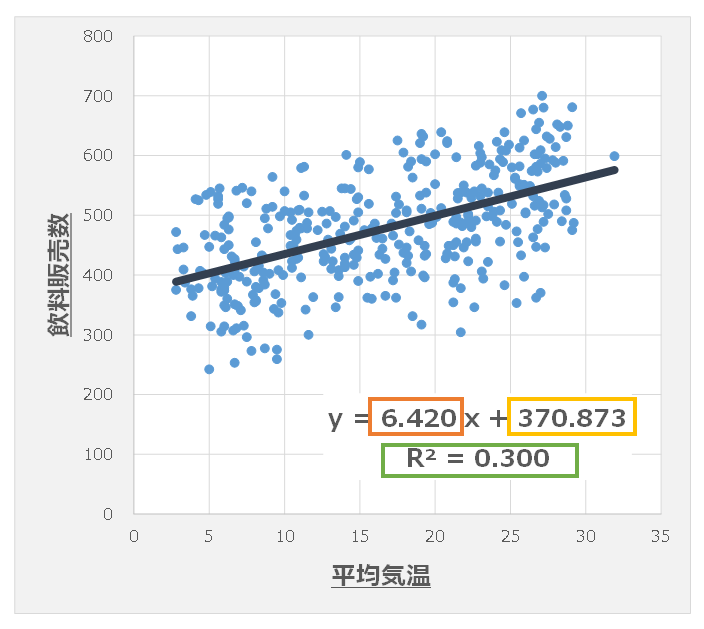
それぞれ同じことを表している数値は、同じ色の枠で囲っています。

この回帰式からは「平均気温が１℃上がると、飲料販売数が6.4205本上がるだろう」ということが読み取れます。
ただ、この式が出たからOKではなく、この回帰式の精度を評価しなくてはいけません。

それが評価できるのが緑枠のR²です。これは回帰式の”当てはまりの良さ”や説明変数が目的変数を”どれくらい説明できているか”を表す、『決定係数』といいます。

「０～１」の値を取り、１に近いほど、回帰式の当てはまり（予測性能）が良いとされます。
今回の場合は、「0.3004(30.04％)」と高くない数値のため、この回帰式にはあまり予測性能がないといえます。

では、「飲料販売数」を「平均気温」で予測すること、また因果関係を仮定したことは間違いだったのでしょうか。それがわかるのが、赤枠の数値です。

中段の数値は、「十分ゼロに近ければ、ほぼ確実に効果のある説明変数があり、意味のある回帰式である」という解釈ができます。

下段の数値は、「十分ゼロに近ければ、ほぼ確実に効果のある説明変数である。」という解釈ができます。
（※十分にゼロに近いかどうかの判断は、一般的に0.05未満かどうかで判断します）
※単回帰分析の場合、この2つの赤枠の数値は同じ値になります。次の重回帰分析では違う値になります。

今回の場合では十分ゼロに近いため、「平均気温」は「飲料販売数」を説明するのに効果のある変数であることが統計的に示すことができています。
ただ、回帰式の決定係数（上記の緑の枠）は高くないため、「平均気温」だけでは「飲料販売数」を予測することは難しいのではないかという結論になります。

では、「平均気温」だけでは難しいのであれば、他の変数も入れて予測できないかを次に考えてみます。

○重回帰分析の例
先ほどの例の延長として、重回帰分析を行っていきます。

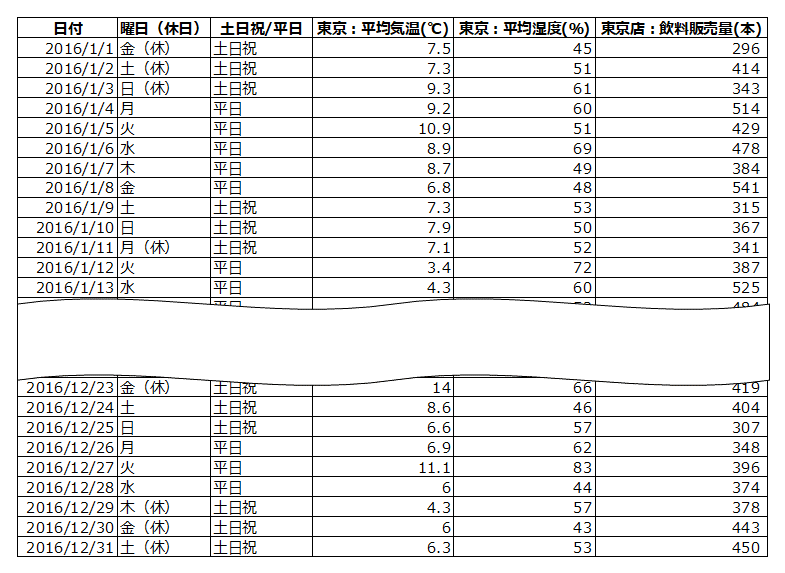
今回は飲料販売数に影響があるであろう変数に、「平均湿度」と「土日祝かどうか」を入れます。
　目的変数：飲料販売数
　説明変数：平均気温、平均湿度、土日祝日かどうか

---

---

○ダミー変数について
「土日祝日かどうか」という変数は、数値ではありません。
そのため、ダミー変数として数値変換をする必要があります。
今回の場合は、『土日祝：1、平日：0』として数値変換を行っています。

---

---

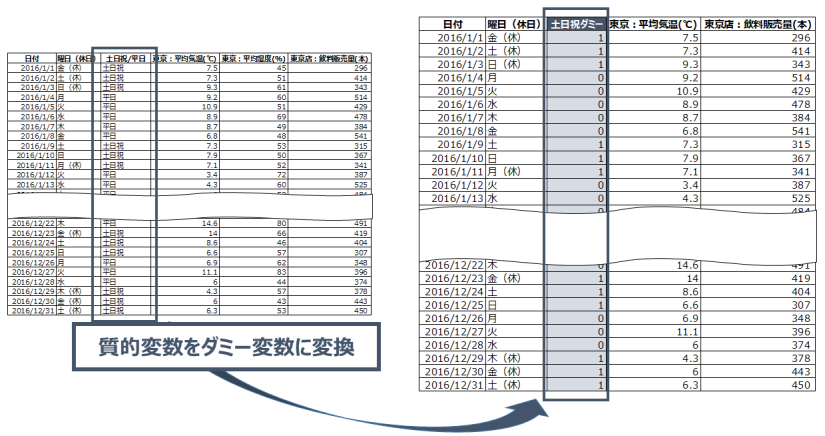
重回帰分析の場合は変数が沢山あるため、エクセルなどで散布図を描くことができません。
そのため、エクセルで重回帰分析をする場合は『分析ツール』で行います。

行った結果は次の通りです。

---

---

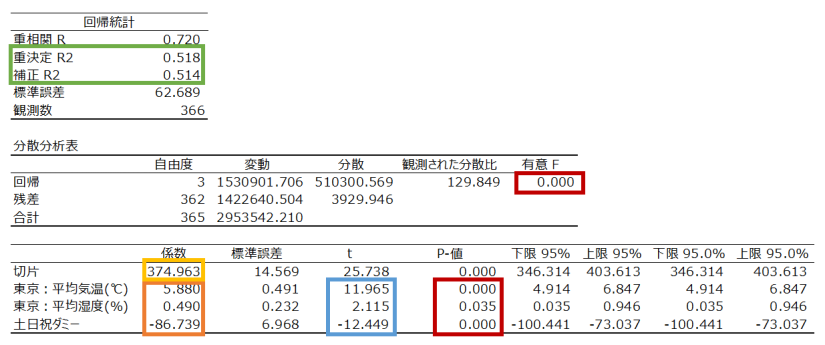
回帰式で表すと以下のようになります。（オレンジと黄色の値が回帰係数です。）
（飲料販売数）＝　5.880*（平均気温）＋0.490*（平均湿度）－86.739＊（土日祝ダミー）＋374.963

さて次に、この回帰式の精度とその妥当性、回帰係数の妥当性と各説明変数の目的変数への影響度を確認していきます。

・回帰式の精度と妥当性
この回帰式の決定係数（上記の緑枠）は「0.518」なのですが、重回帰分析の場合はその下の”補正R2”という値で、回帰式の当てはまり具合を判断します。

決定係数は説明変数の数が増えるほど1に近づくという性質を持っています。そのため、説明変数の数が多い場合には、この点を補正した「”補正R2”＝自由度調整済み決定係数」を使います。

次に中段の赤枠の数値は、「十分ゼロに近いため、効果のある説明変数があり、統計的に意味のある回帰式である」と解釈できます。（※十分にゼロに近いかどうかの判断は、一般的に0.05未満かどうかで判断します）

・回帰係数の妥当性と影響度
下段の赤枠の数値も、「十分ゼロに近いため、効果のある（意味のある）説明変数である。」と、それぞれの説明変数が解釈できます。（※十分にゼロに近いかどうかの判断は、一般的に0.05未満かどうかで判断します）

影響度については、青枠の数値で判断します。今回の場合であれば「土日祝日ダミー」が ”-12.449” と絶対値が最も大きいため、影響度が大きいと判断することができます。

・説明変数を追加して良かったのか
これを判断できるのは、「”補正R2”＝自由度調整済み決定係数」です。

---

---

説明変数が「平均気温」のみだった時が「0.298」だったのに対して、説明変数に「平均湿度」と「土日祝かどうか」を追加したときには「0.514」だったため、追加したことで精度が上がったと判断できます。

ただ、「0.514」では目的変数の半分くらいを3つの説明変数で表現できているという状態のため、精度向上のためにまだまだ検討の余地は残っていそうです。

回帰分析をこれからも身近に

回帰分析は、統計的分析手法の中で、ビジネスで一番使われている手法かと思います。
エクセルなどで簡単に実施でき、アンケートデータの分析や、コールセンターの入電予測など、身近で手元にあるデータを使って、効果の検証や未来の予測ができるのが理由かと思います。

そして、誰でも使っているからこそ、差がつくのは分析の前後の部分と分析の正しい解釈です。
”前”というのは、課題の設定方法や、仮定の置き方
”後”というのは、出てきた分析結果から、どのような施策に繋げるか　です。

総務省統計局が公開している以下の例では、この前後の部分が上手く設計されています。
https://www.stat.go.jp/dstart/point/seminar1/

なお、”分析の正しい解釈”について、今回の記事が皆様のお役に立てれば幸いです。

参考文献
・多変量解析法入門 （ライブラリ新数学大系）
・総務省 ICTスキル総合習得プログラム
・DataStart（総務省統計局）
・統計Web

---