300円で最も満足できるおやつの組み合わせは？～数理最適化の話～

今回はデータ分析手法の一つである「数理最適化」のお話しをします。
「統計」や「機械学習」に比べると、一般的な認知度は低い「数理最適化」ですが、そのポテンシャルは非常に大きいです。

数理最適化とは

数理最適化とは、複数の制約条件を全て満たしながら、目的を達成させることが出来る組合せを大量に試算し、成果の最大化を追求する手法のことをいいます。

こういう風に書くと少し難しそうに見えてしますが、身近な例を挙げながら、どういう問題が解けるのか、「成果の最大化」「制約条件」「試算する組み合わせ」について解説していきます。

身近な数理最適化

例①　遠足にどのお菓子を持っていくか
＝＝
小学生の頃に胸躍ったイベントの一つが、遠足でした。
遠足の嬉しさは２つ。『授業がなくなること』と『お菓子を持っていけること』でした。
ただ、学校の決まりで持っていけるお菓子は、300円までかつ5つまでと決められていました。
そこで一番満足できる組み合わせを考えることにしました。
次の【表.1】は、お菓子の価格とその満足度を表しています。

---

---

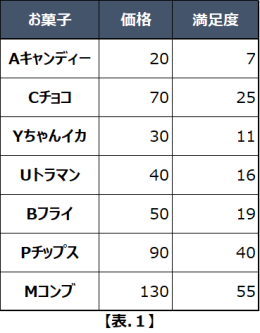
この時、満足度を最大化するお菓子の組み合わせはどうなるでしょうか。
ただし、同じお菓子ばかりだと満足度は下がるので、持っていくのは1種類１つまでとします。

＝＝
この問題を解けるのが、『数理最適化』の手法です。
また、上記の「成果の最大化」「制約条件」「試算する組み合わせ」についてまとめると、【表.2】のようになります。

---

---

この問題は、プログラムに任せると一瞬で答えを出してくれますが、ここではそれでは味気ないので、実際の「お菓子の組み合わせ」を確認しながら解いていきましょう。

例①の解法
・すべての「組み合わせ」
はじめに、“持っていくのは1種類１つまで” という制約条件は、言い換えると、それぞれのお菓子は「持っていく / 持っていかない」であることを指しています。

---

---

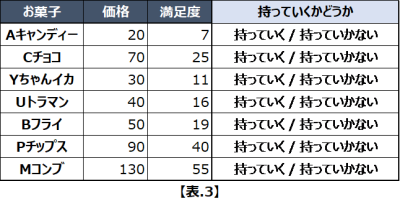
このとき他の制約条件である「お菓子の合計金額300円以内」と「お菓子の数は5つまで」を無視したお菓子の組み合わせは、
　お菓子の選び方＝「持っていく / 持っていかない」＝2通り
　お菓子の種類＝７つ
なので、128通り（2通りの7乗）となります。

「持っていく」　　　=　１
「持っていかない」　=　０
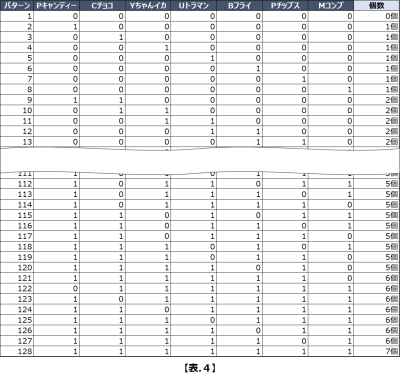
として、すべての通りを表形式で表すと【表.４】のようになります。

パターン１を見て頂くとわかる通り、128通りの中には『全部を持って行かない』というパターンが含まれているため、実際に試算する組み合わせ数は127通りとなります。

---

---

・他の制約条件をかける
さて、ここからは【表.４】に対して制約条件をかけていきます。

「持っていくお菓子の数は５つまで」
【表.4】の個数を１個から5個までにフィルター（127通り⇒119通り）

---

---

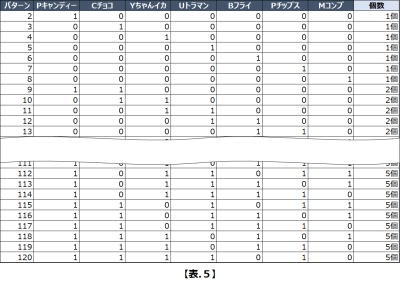
・「持っていくお菓子の価格の合計が300円まで」
各パターンの合計価格を求めて、列を以下のように追加し、その合計価格を300円以下でフィルターをかけます。（119通り⇒102通り）

---

---

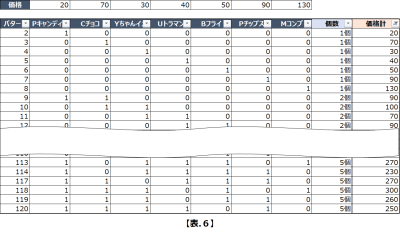
・「成果の最大化」
【表.６】までで、試算する組み合わせに対する「制約条件」は全てかけ終わったので、この中から「成果を最大化する」パターンを見つけます。
今回の場合だと、「満足度」が最大になるパターンを見つけたいので、【表.６】に「満足度」列を追加して計算し、降順で並び替えると以下のようになります。

---

---

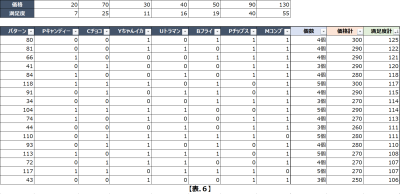
ということで、今回の問題の答えとしては
「Yちゃんイカ、Bフライ、Pチップス、Mコンブ」の4つを持っていくとき、満足度が一番高くなる（満足度：125）となります。

例②　ダイエットの計画を立てる
健康診断を終えるといつも「ダイエットしなきゃ...」と思うものの、好きなものは食べたいし、運動する時間はなかなか取れずにいます。
また、極端に断食とかをしてしまうと必要な栄養が取れなくて、逆に病気になっちゃうのではと余計なことを考えてしまいます。

＝＝
この問題、数理最適化なら解けます。
このわがままな要望をまとめると『必要な栄養は取りつつ、1日のカロリー摂取量は規定範囲に抑え、なるべく好きなものを食べるようにするにはどうすればいいだろうか。』となります。

その上で例①と同じように、「成果の最大化」「制約条件」「試算する組み合わせ」についてまとめると【表.7】のようになります。

---

---

今回はダミーデータですが、この問題設定の場合、【表.8】のようなデータがあれば、例①と同じような手法を使って、『なるべく好みのものを食べながら、栄養素を確保でき、カロリーも抑えることができる』ダイエット計画を立てることができます。

---

---

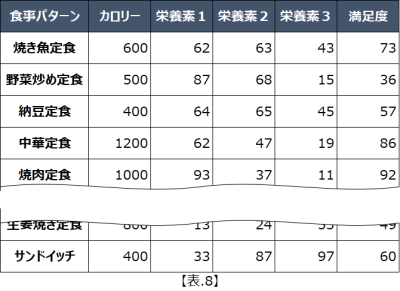
ビジネスの場面での数理最適化

●シフティング
看護師やコールセンター等のシフト調整では、最低必要人数の担保、スタッフのスキル、希望する休日などを考慮に入れた上で、従業員やクライアントへの満足度（品質）を一定以上保ちながら、コストを最小化するシフトを作成する。

●生産計画
製造業の場面では、供給が必要な商品の生産量を保ち、かつ在庫や輸送のコストを最も少なくするために、どのくらいの量をどの工場でどの順序で生産するのが望ましいか、という組み合わせを計算する。

●輸送計画
運送業の場面では、定められた配送時間を守り、配送に必要な時間、数多くある店舗をどのような順序で巡るのが最も短時間で済むか、という日々のトラックごとの巡る順番を計算する。

この例の他にも、「様々な制約条件のもと、最も成果が上がるための組み合わせを考える」場面であれば、幅広く活用できるのが数理最適化の技術です。

そもそも、数ある制約条件のもと、今ある資源を活用して成果を上げることが経営判断の1つであるため、ビジネスと数理最適化の親和性は高いのです。

数理最適化は問題設定が一番大変

ここまで読んでいただくと、数理最適化の手法を使おうと思うと、「成果の最大化」「制約条件」の設定が非常に重要であることがわかると思います。

一方で、数理最適化を解くのはコンピュータなので、「成果の最大化」「制約条件」を数値や式で表す必要があり、とても大変な場合が多いです。

例えば、初めに挙げた例２つの『満足度』という数値は、なかなか数値化するのが難しいものです。
今回のような自分の満足度であれば、自分の感覚でつければいいです。

しかし、”お客様の満足度” となると、満足度が高い状態とはどういうことなのか、という定義がしっかりしていないと意味のない結果になってしまう場合があります。

また、「制約条件」については、すべての制約を洗い出す必要があります。

これも先ほどの例②から考えると、朝昼晩の食事パターンの設定でしたが、『朝から焼肉定食を食べる』という選択はあまりしないと思いますし、選択した場合に満足度は下がることが考えられるため、このことを制約条件に追加する必要があります。

また、「三食同じものは食べない」であったり、「前日・前々日食べたものは食べない」というようなことが制約条件に追加されたほうが現実的だと考えられます。

このように、細かいところまで洗い出すことによって、より現実味を帯びた結果を得ることができるのです。

＝＝＝
参考文献
「数理最適化のことはじめ」
「スケジューリング問題とは？数理最適化によるシフト作成などの問題解決事例」
「人間の経験と勘を越える「数理最適化」で、製造業の生産計画から、ひとを解放したお話」

---