ベイズの世界

ベイズ統計とは

ベイズ統計は注目され始めてから久しいです。
そのきっかけを作ったのは、マイクロソフトの元代表のビル・ゲイツ氏でした。今から26年前の1996年に「自社が競争優位に立っているのはベイズ統計によるものだ」と新聞の取材に答えたことが始まりと言われています。

また、2001年の基調講演でも「21世紀のマイクロソフトの戦略はベイズ統計であること」と「世界中からベイズ統計の研究者をヘッドハンティングしたこと」を公言したことも有名な話です。

ここから一気にベイズ統計の流行が始まり、それが流行では終わらず、今日にまで利活用されるようになっています。たとえば、Google検索の自動翻訳システムや、ECサイトの顧客の購買行動や検索行動から顧客のタイプを推定、迷惑メールかどうかの判定など様々です。

特に最近では、ディープラーニングの中に組み込むことで、より精度の高いAIが出来るようになってきています。

そこで今回は、時代の最先端を行く「ベイズ統計」、特に「ベイズ推定」と「ベイズ更新」について、どのようなことができるのかを具体例を用いながらお話ししていきます。

ベイズ推定

それではベイズ統計、ここでは特にベイズ推定を使うと何ができるのかを見ていきましょう。

いきなりですが、次の問題を考えてみましょう。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
問題１：病気の真の罹患率

１万人に１人だけがかかる難病があるとします。
この難病にかかっているかどうかを検査する方法があり、
『実際にこの難病に罹っている人』（＝罹患者）は99パーセントの確率で陽性と診断されます。
一方、『実際にこの難病に罹っていない人』（＝非罹患者）が陽性と誤診される確率は２パーセントです。
さて、この検査をあなたが受けて陽性反応が出た場合、
あなたがその難病に罹っている確率は99パーセントだと判断すべきでしょうか。
（※数値はすべて架空のものです。）
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
「はい」か「いいえ」か、少しお考え下さい。
・
・
・
・
・
・
・
・
・
・
・
・

答えは「いいえ」です。

もしも、本当に「自分が難病である確率が99パーセント」ならば、あなたは相当悲観すると思います。実際、私はこの問題をはじめに見たときは、直感的に「検査しているんだから99パーセントなんじゃないの？」と思っていました。

しかし、実際は「陽性」という結果から「あなたが難病である確率」を推定すると、そこまで高い数値ではないのです。そして、この「陽性」という『結果』から「難病である」という『原因』にさかのぼる推定こそが、ベイズ推定です。

では、実際にベイズ推定を使いながら、「陽性」という結果から「あなたが難病である確率」を求めていきましょう。
なお、本記事では、ベイズの公式などの数式は用いず、『完全独習 ベイズ統計学入門』を参考に、「面積図で図解する」という方針を取っています。

■前提条件の整理

求めていく前に、前提条件を表や図を使って、整理していきます。

①検査しない状況での難病である確率
この確率は問題文冒頭の「１万人に１人だけがかかる難病があるとします。」の通り、
1/10,000　＝　0.01％　です。
そのため、難病でない確率は
1－0.01％　＝　99.99％　となります。

ここではあまり意味のないように見えると思いますが、図にすると以下のようになります。
（※見やすくしているので、辺の長さの比率は気にしないでください。）

---

②検査の精度の確率
検査の精度に関しては、「罹患者」「非罹患者」それぞれで問題文に書かれています。

・罹患者への検査の精度
問題文：「この難病の罹患者に対して行うと99パーセントの確率で陽性かどうかを判別できる検査があります。」

これは、「難病の罹患者」の場合、検査で陽性と出る確率は99パーセントというのは、99パーセントの正確さを持って難病を検出できるということです。その逆に、１パーセントの確率で誤診（実際は罹患しているのに、罹患していないと検査結果が出る）が発生することを表しています。

難病の罹患者が検査で陽性となる確率　：99.0％
難病の罹患者が検査で陰性となる確率　：1.0％


・非罹患者への検査の精度
問題文：「この検査は難病の非罹患者が陽性と誤診される確率は２パーセントです。」

これは、「難病の非罹患者」の場合、間違って陽性と検出される（誤診である）のが２パーセントです。そのため、正確に罹患していないと検出されるのは98パーセントとなります。

難病の非罹患者が検査で陽性となる確率：2.0％
難病の非罹患者が検査で陰性となる確率：98.0％

この2つを表にまとめると以下のようになります。

---

---

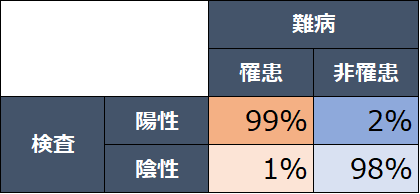
この表から読み取れるのは、（どのような検査でもそうですが）検査は完ぺきなものではなく、リスクがあるということです。

この場合のリスクとは、
「難病なのに難病でないと診断される」場合と、
「難病でないのに難病であると診断される」場合の２つです。

さて、これで前提条件の整理は終わりました。
次からは、図を使いながら「陽性」という結果から「あなたが難病である確率」を求めていきます。

■「陽性」という結果から「あなたが難病である確率」

・（図.１）に②の条件を加える
①は検査をしていない状況での「難病の罹患者」「難病の非罹患者」の確率を図示したものでした。
一方、②は「難病の罹患者」「難病の非罹患者」である条件の下、検査をすると「陽性」「陰性」の診断が出る確率でした。

そこで、①の（図.１）に②の条件を加えると、

難病の罹患者である確率：0.01％⇒陽性（99%）と陰性（1%）にわける
難病の非罹患者である確率：99.99%⇒陽性（2%）と陰性（98％）にわける

ということができ、次の（図.２）のように書き加えることができます。

---

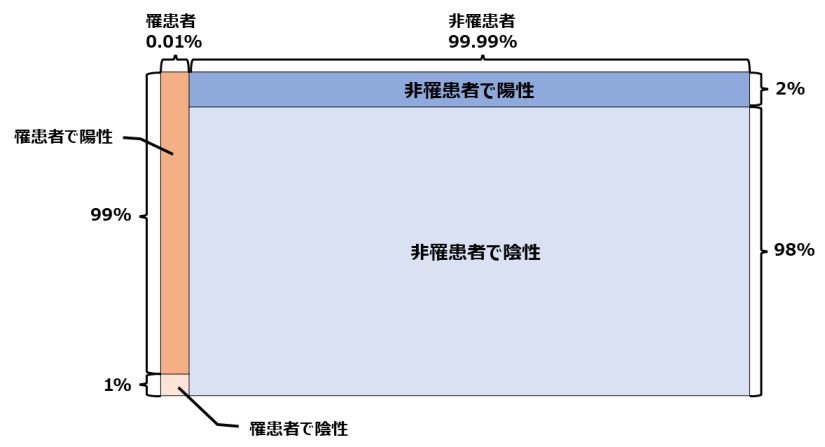
これによって問題文にあった、

＝＝＝
１万人に１人だけがかかる難病があるとします。
この難病の罹患者に対して行うと99パーセントの確率で陽性かどうかを判別できる検査があります。
ただし、この検査は難病の非罹患者が陽性と誤診される確率は２パーセントです。
＝＝＝

という条件すべてが同じ図の中に表現することができました。


・４つの出来事の確率を求める
（図.２）によって、問題文条件すべてを同じ図の中に表現できました。次に４つの出来事の確率を求めてみましょう。
簡単なので数式は省きますが、各確率はそれぞれの確率をかけ合わせれば求めることができます。

---

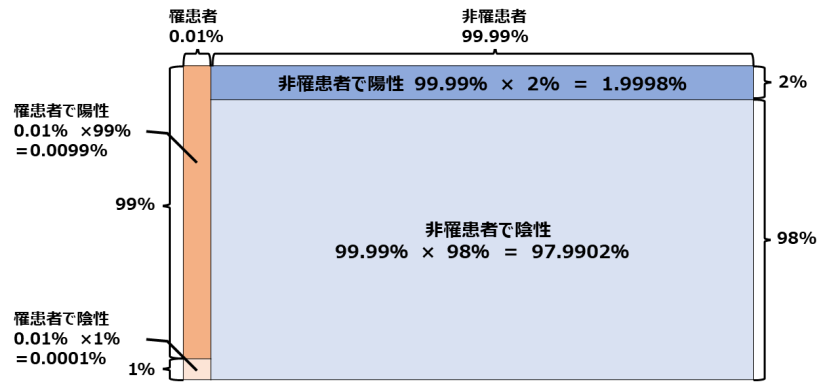
これで、準備のすべてが整いました。


・「陽性」という結果から「あなたが難病である確率」を求める
あなたは今、検査を受けて「陽性」と診断されています。
そのため、（図.３）の中でも、「陽性」であるという領域だけを残すと、次の（図.４）のようになります。

---

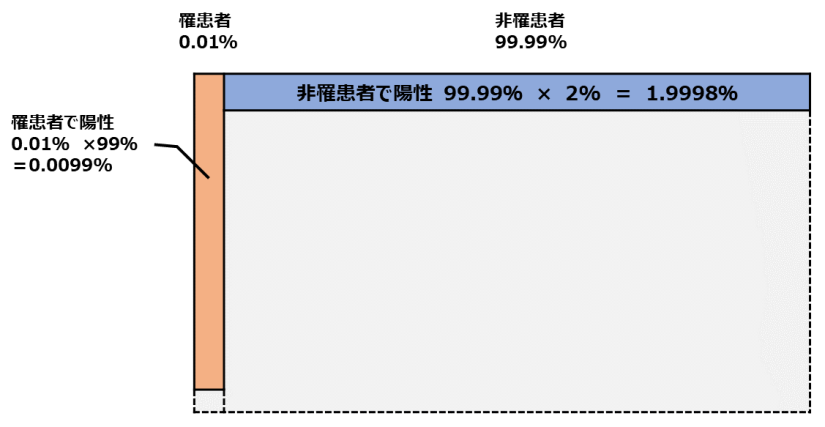
このうち、「難病である確率」を求めると、数式と確率は以下のようになります。

---

この「0.493%」というのが、今回求めたかった「陽性」という結果から「あなたが難病である確率」となります。

■出てきた確率の解釈

『たったの0.493%？？』という感想を持たれた方が多いのではないでしょうか。

はじめに否定した通り、「難病に罹っている確率は99パーセントだと判断すべき」どころか、感覚的にすごく低い確率が出てきていると思います。

ではなぜ、こんなにも低い確率が出てきているかというと、もともと難病の罹患者が非常に稀（１万人に１人）で、非罹患者が圧倒的に多いので、非罹患者を陽性と誤診してしまうことが無視できないほど大きい数値のためです。

『じゃあそもそも、検査する意味がないのではないか？』というと、そうではないのです。

というのも、検査をする前の難病の罹患率は『0.01％』に対して、「陽性」という結果から「難病である確率」は『0.493%』と、約49倍に跳ね上がっています。

これは、「１万人に１人」が「203人に１人」となり、無視するのは得策ではないと判断する人が多くなるのではないでしょうか。

ベイズ更新

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
問題２：再検査による病気の真の罹患率

さて、あなたはある難病の検査を受けて、「陽性」と診断されました。
これまでの話から、「そこまで悲観する必要はないが、この結果は無視できないな」と判断しました。
そこで、問題１と同じ検査をもう一度受けてみると、再度「陽性」と診断されました。
難病に罹患している確率はどれぐらいになるでしょうか。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この問題は次のように考えることができます。

まず、１度目の検査のとき、検査前の難病に罹患している確率は0.01％でした。
しかし２度目の検査では１度目の検査で既に陽性が出ているため、現段階で難病に罹患している確率は 0.01％ではなく、 前回の「陽性」という結果から「難病である確率」である、0.493%になります。

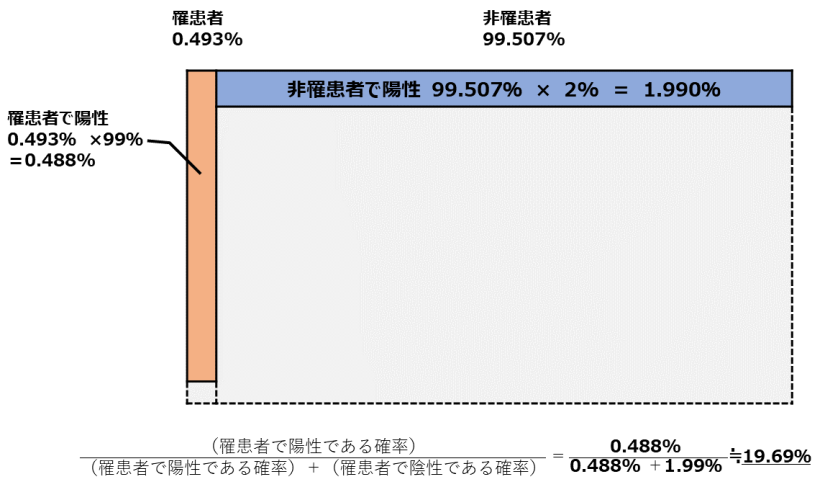
これを上記と同じように（0.01%のところを0.493%に変えて）計算すると、以下の（図.５）から、（数式.２）と計算でき、２回連続で「陽性」と診断されると「難病である確率」は19.69％まで上昇します。

---

さて、このように１度前のベイズ推定で得られた確率を使って、もう一度ベイズ推定することを『ベイズ更新』といいます。

このベイズ更新は、コンピューターの処理能力が向上して、ビッグデータを扱えるようになった今、ベイズ統計が再脚光を浴びるようになった主な要因の １つです。

なぜなら、これを行うために必要なのは、新しいデータ（今回の場合であれば『２回目の検査が陽性であったこと』）と前回求めた『前回の「陽性」という結果から「難病である確率」』だけであるため、以前のデータをすべて保管しておく必要はないからです。

そのため計算を高速に行えますし、データを失うリスク心配することもありません。

”普通の統計”ではなかなかそうはいきません。なぜなら、”普通の統計”の確率で再計算を行うには、過去の膨大なデータもすべて必要ですし、再計算の度に膨大なデータ量を扱うことになるので、コンピューターにも大きな負担がかかるからです。

さらに、何らかの理由で過去データが失われてしまっていると確率を求めることも出来ません。

最後に

さて、「ベイズ統計」の世界はいかがでしたでしょうか。

今回はまだまださわりの部分しかお伝え出来なかったので、また機会があればさらに深いベイズの世界に触れられればと思います。

---